Joue-moi une chanson sur le décalage Doppler ! (texte)
Désolé, votre navigateur ne prend pas en charge l’élément audio, pensez à le mettre à jour.
Avez-vous remarqué que lorsqu’un véhicule d’urgence avec sa sirène hurlante passe devant vous, le ton que vous entendez change de hauteur ? C’est un exemple de décalage Doppler, et c’est un effet qui est associé à tout phénomène ondulatoire (comme les ondes sonores ou la lumière).
Envisageons le cas où le camion de pompiers est à l’arrêt dans l’allée de la caserne en attendant que les pompiers montent à bord, comme le montre l’image ci-dessous. Si la sirène est allumée, un auditeur situé à une certaine distance sur la droite percevra la sirène à la même fréquence que celle à laquelle elle est émise. En fait, une autre personne immobile située sur le côté gauche du camion entendrait également la même tonalité.
(Crédit : Imagine the Universe de la NASA)
Voyons maintenant comment cette situation change lorsque le camion se déplace vers l’observateur immobile avec une vitesse constante, v, comme illustré ci-dessous.
(Crédit : Imagine the Universe de la NASA)
La fréquence de la sirène du camion de pompiers telle qu’entendue par une personne à bord du camion de pompiers n’a pas changé ! Cependant, les ondes dans la direction du mouvement du camion se regroupent car le camion de pompiers rattrape ses propres ondes sonores. Les variations de pression, qui sont représentées par les ondes sinusoïdales, frappent le tympan de l’observateur immobile à une fréquence plus élevée. L’observateur stationnaire à droite perçoit donc une tonalité plus élevée que celle réellement émise par le camion de pompiers.
Notez que les ondes derrière le camion de pompiers (à gauche du schéma) sont étalées car la sirène s’éloigne de son propre son. Cela amènerait un observateur immobile à gauche du camion à percevoir une diminution de la fréquence du de la sirène.
Pour une source se déplaçant vers la droite, un observateur immobile à droite percevrait un son plus élevé et un observateur à gauche percevrait un son plus faible.
La fréquence décalée Doppler non relativiste d’un objet se déplaçant à la vitesse v par rapport à un observateur immobile, est :
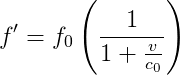
et on peut montrer que la longueur d’onde décalée Doppler est :
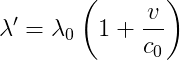
Dans ces deux équations, c0 est la vitesse de l’onde dans un milieu stationnaire (la vitesse du son dans ce cas), et la vitesse est la composante radiale de la vitesse (la partie en ligne droite à partir de l’observateur). Ces deux formules sont des approximations non relativistes qui sont vraies tant que la vitesse de l’objet en mouvement est bien inférieure à la vitesse de la lumière.
Par convention, la vitesse est positive si la source s’éloigne de nous et négative si la source se rapproche de l’observateur.
Donc :
- si la source s’éloigne (vitesse positive), la fréquence observée est plus faible et la longueur d’onde observée est plus grande (décalage vers le rouge).
- si la source se rapproche (vitesse négative), la fréquence observée est plus élevée et la longueur d’onde est plus courte (décalage vers le bleu).
Comment cela affecte-t-il les spectres des objets distants dans l’Univers ? La lumière subit-elle le décalage Doppler ?
Pensez au spectre de la lumière visible : rouge-orange-jaune-vert-bleu-indigo-violet (ou ROY G. BIV pour faire court). Si le décalage de Doppler fonctionne aussi pour la lumière, alors il doit être possible de se déplacer si rapidement vers un feu rouge qu’il vous apparaîtrait vert ! Vous pourriez trouver astucieux d’utiliser cet argument si vous étiez arrêté pour avoir brûlé un feu rouge. Cependant, l’agent de police pourrait alors vous donner une contravention pour excès de vitesse.
Il s’avère que la lumière provenant de n’importe quelle partie du spectre électromagnétique peut être décalée vers le haut ou vers le bas en fréquence en fonction de votre mouvement relatif par rapport à la source émettrice. Le schéma suivant illustre ce phénomène:
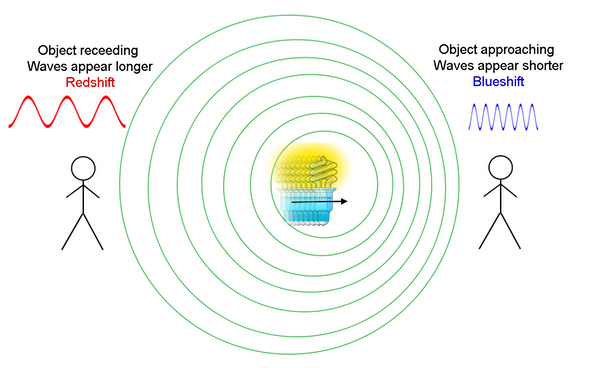
(Crédit : Imagine the Universe de la NASA)
Vous reconnaîtrez qu’il s’agit d’un schéma similaire à celui montrant un camion de pompiers s’approchant de l’observateur immobile, sauf que maintenant la source émet de la lumière au lieu du son. Remarquez que la région où un observateur perçoit une augmentation de la fréquence de la lumière est appelée « décalage vers le bleu », et que la région où l’observateur percevrait une fréquence plus basse (à gauche dans le diagramme) est appelée « décalage vers le rouge. » Il est important de noter que les équations dérivées du décalage Doppler du son fonctionnent également pour les sources lumineuses en mouvement, à condition que ces dernières ne se déplacent pas à la vitesse de la lumière. Si la vitesse relative entre la source émettrice et l’observateur était proche de la vitesse de la lumière, nous devrions tenir compte des effets relativistes ; ainsi, l’équation changerait.
Voir une dérivation mathématique de l’équation du décalage Doppler.
Voir des exemples de spectres décalés vers le rouge pour certaines galaxies.
Questionnez vos connaissances sur le décalage Doppler
Retournez à la résolution de la vitesse de M31 à l’aide de son spectre
.