Calcul de l’impédance
Dans les circuits alternatifs, la loi d’Ohm prend la forme plus générale : E = I⋅Z, où E est la tension et Iest le courant, comme précédemment. Le nouveau terme, Z, est l’impédance,une combinaison vectorielle de :
- Résistance, R (en ohms), avec des chutes de tension en phase avec le courant.
- Réactance inductive, XL (en ohms), avec des chutes de tension précédant le courant de 90°.
- Réactance capacitive, XC (en ohms), avec des chutes de tension retardant le courant de 90°.
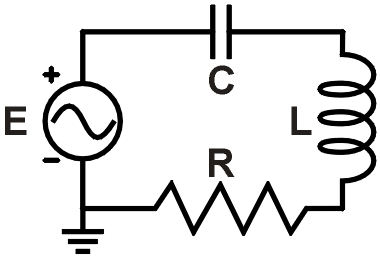
f = 6,4 kHz R = 120 Ω
L = 3,6 mH C = 0,38 μf
Figure 1. Exemple de circuit RLC

Figure 2. La somme vectorielle de R et de
XL-XC donne Z
À partir des formules pour XL et XC, vous pouvez voir que les réactances dépendent à la fois des valeurs des composants L et C,ainsi que de la fréquence alternative, f :
![]() et
et 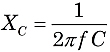
où f est la fréquence enHertz (ou sec-1), L est l’inductance en Henries, et C lacapacité en farads. Parce que XL et X ont une phase différente de 180°, la réactance totale X d’un circuit en série est XL-XC.
Les utilisations familières de la loi d’Ohm, telles que les calculs de circuits en série et en parallèle, s’appliquent toujours. Cependant, vous devez maintenant considérer les contributions vectorielles concurrentes des résistances et des réactances.
Angles de phase et vecteurs
Trouvons l’impédance totale du circuit de la figure 1. En utilisant les formules ci-dessus :
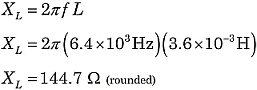 |
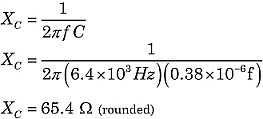 |
Construire l’impédance Z, la résistance contribue à la composante horizontale. La composante verticale est la différence des réactances : XL-XC.Alors, Z est la somme vectorielle de R et XL-XC,comme illustré dans la figure 2.
Dans la figure 2, voyant que Z est l’hypoténuse d’un triangle rectangle,nous pouvons utiliser le théorème de Pythagore et la géométrie du triangle rectangle pour évaluer Z.
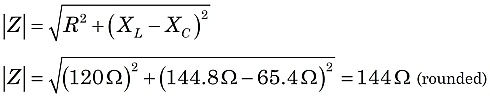
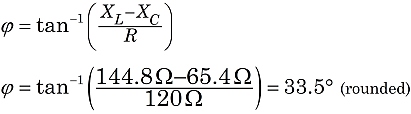
Donc, dans ce circuit, nous assisterions à l’effet d’une impédance de144 ohms, le courant étant en retard sur la tension d’alimentation avec un angle de phase de 33.5°.
Comme vous pouvez le deviner à partir de la discussion ci-dessus, il est tout à fait possible que les réactances inductive et capacitive s’annulent exactement sous les bonnes combinaisons de valeurs de L, C et f. C’est une condition très importante connue sous le nom de résonance.
.