Schrijf formules voor binaire ionische verbindingen
Als je de elementen kent die een binaire ionische verbinding vormen, kun je de formule schrijven. Begin met het metaalion en zijn lading, gevolgd door het niet-metaalion met zijn lading. Omdat de totale verbinding elektrisch neutraal moet zijn, bepaal je hoeveel ionen van elk type nodig zijn om ervoor te zorgen dat de positieve en negatieve ladingen elkaar opheffen. Beschouw de verbinding aluminiumnitride. De ladingen van elk van deze ionen kunnen worden bepaald door te kijken naar de groepen waarin aluminium en stikstof voorkomen op het periodiek systeem. De ionen zijn:
Aangezien de ionen ladingen hebben die even groot zijn (3, maar verschillende tekens), is 1:1 de laagste verhouding van ionen die een neutrale verbinding oplevert. Aangezien de lading van aluminium 3+ is en de lading van stikstof 3+, is de som van hun ladingen nul (+3+; -3=0). De formule van aluminiumnitride is dus aluminiumoxide. Een andere verbinding, lithiumoxide, bevat de volgende ionen:
In dit geval zijn twee lithiumionen, elk met een 1+ lading, nodig om de lading van elk oxide-ion, dat een (2-)lading heeft, uit te balanceren. De formule van lithiumoxide is lithiumoxide, omdat de verbinding neutraal moet zijn. Voor verbindingen waarbij de verhouding tussen de ionen niet zo duidelijk is, is een alternatieve manier om de juiste formule te bepalen de “kriskras”-methode. In deze methode kruist de numerieke waarde van elke lading om het subscript van het tegenovergestelde ion te worden. De tekens van de ladingen vallen weg. De kriskrasmethode wordt hieronder gedemonstreerd voor aluminiumoxide.
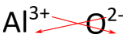
De rode pijlen geven aan dat de 3 van de lading (3+) overgaat in het subscript van \(O), terwijl de 2 van de lading (2-) overgaat in het subscript van \(Al). De formule voor aluminiumoxide is \(\ce{Al_2O_3}\).
Voor aluminiumoxide levert de kriskras-methode direct de juiste formule op, maar in sommige gevallen is een andere stap nodig. Omdat ionische verbindingen altijd beschreven worden door hun empirische formules, moeten ze geschreven worden als de laagste gehele getalsverhouding van de ionen. In het geval van aluminiumnitride zou de kriskras-methode een formule opleveren van {Al_3N_3}, wat niet juist is. Er moet een tweede stap worden uitgevoerd waarbij de subscripts worden gereduceerd maar de verhouding gelijk blijft. \Ô(Ôce{Al_3N_3}Õ) kan worden gereduceerd tot Ô(Ôce{AlN}Õ), omdat beide formules een 1:1 verhouding van aluminiumionen en nitride-ionen beschrijven. Het volgen van de kriskrasmethode om de formule voor lood(IV)oxide te schrijven zou de volgende stappen inhouden:
Sommige overgangsmetalen kunnen meer dan één mogelijke lading hebben. Wanneer dit gebeurt, wordt de lading van het overgangsmetaalkation tussen haakjes in de naam opgenomen. Bijvoorbeeld, lood(IV) oxide heeft \(\ce{Pb^{4+}} als metaalkation.
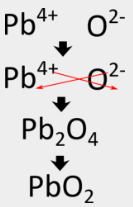
De kriskrasmethode geeft eerst \(\ce{Pb_2O_4}}) voor de formule, maar dat moet worden herleid tot \(\ce{PbO_2}}), wat de juiste formule is.