Dans les applications d’ingénierie, nous rencontrons fréquemment des fonctions dont les valeurs changent brusquement à des valeurs spécifiées du temps t. Un exemple courant est lorsqu’une tension est activée ou désactivée dans un circuit électrique à une valeur spécifiée du temps t.
Plus tard, sur cette page…
Fonction à pas unitaire décalé
Impulsion rectangulaire
La valeur de t = 0 est généralement prise comme un moment commode pour allumer ou éteindre la tension donnée.
Le processus de commutation peut être décrit mathématiquement par la fonction appelée fonction de pas unitaire (autrement appelée fonction de Heaviside d’après Oliver Heaviside).
La fonction de pas unitaire
Définition : La fonction de pas unitaire, `u(t)`, est définie comme
`u(t)={ : {(0, t < 0), (1, t > 0) :}
C’est-à-dire que u est une fonction du temps t, et u a pour valeur zéro lorsque le temps est négatif (avant qu’on actionne l’interrupteur) ; et pour valeur un lorsque le temps est positif (à partir du moment où on actionne l’interrupteur).
Graphe de `f(t)=u(t)`, la fonction à pas unitaire.
Valeur à t = 0?
Dans certains manuels, vous verrez la fonction à pas unitaire définie comme ayant la valeur 1 à t = 0, comme suit :
`u(t)={ : {(0, t < 0), (1, t >= 0) :}
Nous indiquerions la discontinuité sur notre graphe de la manière suivante :
Graphe de `f(t)=u(t)`, la fonction à pas unitaire, avec `f(0) = 1`.
Egalement, vous verrez parfois la valeur donnée comme `f(0) = 0.5`.
Dans ce travail, cela ne fait pas une grande différence pour nos calculs, nous continuerons donc à utiliser la première interprétation, et à dessiner nos graphiques en conséquence.
Fonction à pas unitaire décalé
Dans de nombreux circuits, les formes d’onde sont appliquées à des intervalles spécifiés autres que `t=0`. Une telle fonction peut être décrite en utilisant la fonction à pas unitaire décalée (alias retardée).
Définition de la fonction à pas unitaire décalée
Une fonction qui a la valeur `0` jusqu’au moment `t = a` et qui a ensuite la valeur `1`, s’écrit :
`u(t-a)={{ : (0, si, t < a), (1, si, t > a) :}`
Exemple 1 – Fonction à échelon unitaire décalé
`f(t) = u(t – 3)`
L’équation signifie que f(t) a une valeur de 1. équation signifie que f(t) a pour valeur `0` lorsque `t < 3` et `1` lorsque `t > 3`.
Le croquis de la forme d’onde est le suivant :
Graphe de `f(t)=u(t-3)`, une fonction à pas unitaire décalé.
Impulsion rectangulaire
Une situation courante dans un circuit est qu’une tension soit appliquée à un moment particulier (disons t = a) et retirée plus tard, à t = b (disons). Nous écrivons une telle situation en utilisant des fonctions à pas unitaire comme:
`V(t) = u(t – a) – u(t – b)`
Cette tension a une intensité `1`, une durée `(b – a)`.
Exemple 2 – Impulsion rectangulaire
Le graphique de `V(t) = u(t – 1,2) – u(t – 3,8)` est le suivant. Ici, la durée est `3,8 – 1,2 = 2,6`.
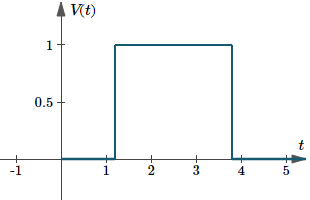
Graphe de `V(t)=u(t-1.2)-u(t-3,8)`, un exemple d’impulsion rectangulaire.
Exercices
Besoin de papier graphique ?
Écrivez les fonctions suivantes en termes de fonction(s) à pas unitaire. Esquissez chaque forme d’onde.
(a) Une source de 12 V est mise sous tension à t = 4 s.
Réponse
Puisque la tension est mise sous tension à t = 4, nous devons utiliser u(t – 4). Nous multiplions par 12 puisque c’est la tension.
Nous écrivons la fonction comme suit :
`V(t)=12-u(t-4)`.
Voici le graphique :
Graphe de `V(t)=12-u(t-4)`, une fonction à pas décalés.
(b) `V(t)={{ : (1, 0 < t < a),(0, t > a) :}`
(On suppose que a > 0.)
Réponse
En clair, la tension a la valeur `1` jusqu’au temps `t = a`. Ensuite, elle est mise hors tension.
Nous sommes dans une situation d' »impulsion rectangulaire » et devons utiliser cette formule :
`V(t) = u(t – a) – u(t – b)`
Dans notre exemple, l’impulsion commence à `t = 0`, on utilise donc `u(t)`, et se termine à `t = a`, on utilise donc `u(t – a)`.
Donc la fonction requise est :
`V(t)=1-` `=u(t)-u(t-a)`
Graphe de `V(t)=u(t)-u(t-a)`, une fonction à pas unitaire décalé.
(c) Un cycle d’une onde carrée, `f(0) = 4`, amplitude = `4`, période = `2` secondes.
Réponse
`f(0) = 4` signifie qu’on commence à la valeur `4`.
Si toute l’onde a une période `2`, et que c’est une onde carrée, alors cela signifie que pendant la moitié du temps, la valeur est (positive) `4` et l’autre moitié, elle est `-4`.
Donc pour la première seconde, elle a la valeur `4`, pour la seconde, la valeur de la fonction est `-4`.
Nous écrivons cela, en utilisant la formule « impulsion rectangulaire » de tout à l’heure :
`f(t) = 4-{u(t) – u(t – 1)}` `-4-{u(t-1) – u(t – 2)}`
`=4-u(t)-8-u(t-1)+4-u(t-2)`
Le graphique de ce premier cycle est :
Graphe de `f(t)=4-u(t)-8-u(t-1)+4-u(t-2)`, une onde carrée.
(d) La fonction rampe unitaire (soit .`f(t) = t` pour `t > 0`)
Réponse
La fonction rampe unitaire a une pente `1`, partant de `t = 0`, et passe par `(0, 0)`.
Donc la fonction tension est donnée par :
`V(t) = t – u(t)`
Le graphe de la fonction est :
Graphe de `V(t)=t – u(t)`, la fonction de rampe unitaire.
(e) Un cycle d’une forme d’onde en dents de scie (i.Soit `f(t)=a/b t` pour `0 < t < b`. On suppose que `a > 0`.)
Réponse
Notre graphe commence à `t = 0` et a une pente `a / b`. Il se termine à `t = b`.
Donc notre fonction sera :
`f(t)=a/b t – {u(t)-u(t-b)}`
Le graphique de notre fonction :
Graphe de `f(t)=a/b t – {u(t)-u(t-b)}`, une forme d’onde en dents de scie.
(f) `V(t)={ { : (0,t < 3), (2t+8,3 < t 5) :}`
Réponse
Dans cet exemple, notre fonction est `V(t) = 2t + 8` qui a une pente `2` et un `V`-intercept `8`.
Le signal n’est allumé qu’entre `t = 3` et `t = 5`. Le reste du temps, il est éteint.
Donc notre fonction de tension sera :
`V(t) ` `= (2t+8) -{u(t – 3)- u(t – 5)}`
Le graphique est le suivant :
Graphe de `V(t) = (2t+8) -{u(t – 3)- u(t – 5)}`. La ligne pointillée correspond à `V(t) = 2t + 8`.
top
Recherche IntMath
Solveur de calcul en ligne
Ce solveur de calcul peut résoudre un large éventail de problèmes mathématiques.
Voir : Solveur de calcul en ligne
.